Το θέμα αυτού του άρθρου είναι ο υπολογισμός ενός πολυανθρακικού θόλου με τα χέρια σας. Πρέπει να μάθουμε πώς να υπολογίζουμε τις κύριες παραμέτρους της δομής που σχετίζονται με την αντοχή και τις διαστάσεις της. Λοιπόν πάμε.

Τι υπολογίζουμε
Πρέπει να μάθουμε να υπολογίζουμε:
- Το πάχος του πολυανθρακικού και το βήμα του κιβωτίου ανάλογα με το αναμενόμενο φορτίο χιονιού ανά τετραγωνικό μέτρο.
- Διαστάσεις καλύμματος τόξου (που ως προς τη γεωμετρία καταλήγει στον υπολογισμό του μήκους του τόξου).
Για να διευκρινίσουμε: διερευνούμε τρόπους υπολογισμού του τόξου για τη γνωστή ακτίνα και γωνία του τομέα, καθώς και για την περίπτωση που γνωρίζουμε μόνο τις αποστάσεις μεταξύ των ακραίων σημείων της επιφάνειας του τόξου.
- Ελάχιστο τμήμα σωλήνα με γνωστό φορτίο κάμψης.
Με αυτή τη σειρά, θα προχωρήσουμε.
Πάχος τόρνου και επίστρωσης
Ας ξεκινήσουμε με τον υπολογισμό του φορτίου χιονιού.
Πριν καταλάβουμε πώς να υπολογίσουμε ένα πολυανθρακικό θόλο, θα διατυπώσουμε μερικές υποθέσεις στις οποίες βασίζεται ο υπολογισμός.
- Τα δεδομένα που δίνονται σχετίζονται με υλικό υψηλής ποιότητας χωρίς σημάδια καταστροφής από την υπεριώδη ακτινοβολία. Το πολυανθρακικό χωρίς φίλτρο UV γίνεται εύθραυστο μετά από 2-3 χρόνια λειτουργίας στο φως.

- Παραβλέπουμε εσκεμμένα την περιορισμένη σταθερότητα παραμόρφωσης του κιβωτίου, θεωρώντας ότι είναι απολύτως ισχυρό.
Και τώρα - ένα τραπέζι που θα σας βοηθήσει να επιλέξετε το βέλτιστο πάχος πολυανθρακικού και το βήμα του κιβωτίου.
| Φορτίο, kg/m2 | Διαστάσεις κυψέλης κιβωτίου με πάχος πολυανθρακικού, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050x750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Αψίδα
Υπολογισμός κατά ακτίνα και τομέα
Πώς να υπολογίσουμε το τόξο για ένα θόλο αν γνωρίζουμε την ακτίνα κάμψης και τον τομέα του τόξου;

Ο τύπος θα μοιάζει με P=pi*r*n/180, όπου:
- Το P είναι το μήκος του τόξου (στην περίπτωσή μας, το μήκος ενός φύλλου πολυανθρακικού ή ενός σωλήνα προφίλ, που θα γίνει στοιχείο του πλαισίου).
- Το pi είναι ο αριθμός "pi" (σε υπολογισμούς που δεν απαιτούν εξαιρετικά υψηλή ακρίβεια, συνήθως λαμβάνεται ίσος με 3,14).
- r είναι η ακτίνα του τόξου.
- n είναι η γωνία τόξου σε μοίρες.
Ας υπολογίσουμε, για παράδειγμα, με τα χέρια μας το μήκος του τόξου του θόλου με ακτίνα 2 μέτρων και τομέα 35 μοιρών.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 μέτρα.
Στη διαδικασία της εργασίας, εμφανίζεται συχνά η αντίθετη κατάσταση: είναι απαραίτητο να ρυθμίσετε την ακτίνα και τον τομέα του τόξου σε ένα σταθερό μήκος του τόξου. Οι λόγοι είναι σαφείς: η τιμή του πολυανθρακικού είναι αρκετά υψηλή για να ελαχιστοποιήσει την ποσότητα των απορριμμάτων.
Προφανώς, στην περίπτωση αυτή το γινόμενο του τομέα και της ακτίνας θα είναι ίσο με P/pi*180.
Ας προσπαθήσουμε να χωρέσουμε το τόξο κάτω από ένα τυπικό φύλλο μήκους 6 μέτρων. 6/3,14*180=343,9 (με στρογγυλοποίηση). Επιπλέον - μια απλή επιλογή τιμών με μια αριθμομηχανή στο χέρι: για παράδειγμα, για έναν τομέα τόξου 180 μοιρών, μπορείτε να πάρετε την ακτίνα ίση με 343,9 / 180 \u003d 1,91 μέτρα. με ακτίνα 2 μέτρων, ο τομέας θα είναι ίσος με 343,9 / 2 \u003d 171,95 μοίρες.
Υπολογισμός με συγχορδίες
Πώς φαίνεται ο υπολογισμός του σχεδιασμού ενός πολυανθρακικού θόλου με τόξο αν έχουμε πληροφορίες μόνο για την απόσταση μεταξύ των άκρων του τόξου και του ύψους του;
Σε αυτή την περίπτωση, εφαρμόζεται ο λεγόμενος τύπος Huygens. Για να το χρησιμοποιήσουμε, ας διαιρέσουμε διανοητικά τη χορδή που συνδέει τα άκρα της καμάρας στο μισό, μετά από την οποία σχεδιάζουμε μια κάθετη προς τη χορδή στη μέση.
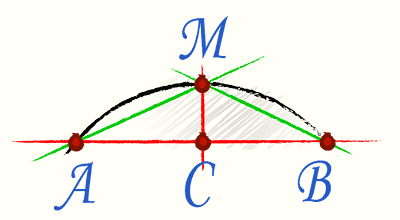
Ο ίδιος ο τύπος έχει τη μορφή Р=2l+1/3*(2l-L), όπου l είναι η χορδή AM και L είναι η χορδή ΑΒ.
Σημαντικό: ο υπολογισμός δίνει ένα κατά προσέγγιση αποτέλεσμα. Το μέγιστο σφάλμα είναι 0,5%. Όσο μικρότερος είναι ο γωνιακός τομέας του τόξου, τόσο μικρότερο είναι το σφάλμα.
Ας υπολογίσουμε το μήκος του τόξου για την περίπτωση που AB \u003d 2 m και AM - 1,2 m.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 μέτρα.
Υπολογισμός του τμήματος με γνωστό φορτίο κάμψης
Αρκετά μια κατάσταση ζωής: μέρος του θόλου είναι μια προσωπίδα γνωστού μήκους. Μπορούμε να υπολογίσουμε χονδρικά το μέγιστο φορτίο χιονιού σε αυτό. Πώς να επιλέξετε έναν σωλήνα προφίλ ενός τέτοιου τμήματος για δοκούς έτσι ώστε να μην λυγίζει υπό φορτίο;

Σημείωση! Εσκεμμένα δεν θίγουμε τον τρόπο υπολογισμού του φορτίου στο θόλο. Η αξιολόγηση του φορτίου χιονιού και ανέμου είναι ένα εντελώς αυτάρκης θέμα για ένα ξεχωριστό άρθρο.
Για να υπολογίσουμε, χρειαζόμαστε δύο τύπους:
- M = FL, όπου M είναι η ροπή κάμψης, F είναι η δύναμη που εφαρμόζεται στο άκρο του μοχλού σε κιλά (στην περίπτωσή μας, το βάρος του χιονιού στο γείσο) και L είναι το μήκος του μοχλού (το μήκος της δοκού που φέρει το φορτίο από το χιόνι, από άκρη σε σημείο συνδετήρες) σε εκατοστά.
- M/W=R, όπου W είναι η ροπή αντίστασης και R η αντοχή του υλικού.
Και πώς θα μας βοηθήσει αυτός ο σωρός άγνωστων αξιών;
Από μόνο του, τίποτα. Λείπουν ορισμένα δεδομένα αναφοράς για τον υπολογισμό.
| ποιότητας χάλυβα | Αντοχή (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15 GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10 HSND | 3400 |
Αναφορά: Οι χάλυβες St3, St4 και St5 χρησιμοποιούνται συνήθως για επαγγελματικούς σωλήνες.
Τώρα, με βάση τα δεδομένα που έχουμε, μπορούμε να υπολογίσουμε τη ροπή αντίστασης κάμψης του σωλήνα προφίλ. Ας το κάνουμε.
Ας υποθέσουμε ότι 400 κιλά χιονιού συσσωρεύονται σε ένα κουβούκλιο δύο μέτρων με τρεις δοκούς ρουλεμάν από χάλυβα St3.Για να απλοποιήσουμε τους υπολογισμούς, θα συμφωνήσουμε ότι ολόκληρο το φορτίο πέφτει στην άκρη της προσωπίδας. Προφανώς, το φορτίο σε κάθε δοκό θα είναι 400/3=133,3 kg. με ένα μοχλό δύο μέτρων, η ροπή κάμψης θα είναι ίση με 133,3 * 200 \u003d 26660 kgf * cm.
Τώρα υπολογίζουμε τη ροπή αντίστασης W. Από την εξίσωση 26660 kgf * cm / W = 2100 kgf / cm2 (αντοχή χάλυβα) προκύπτει ότι η ροπή αντίστασης πρέπει να είναι τουλάχιστον 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Πώς θα μας οδηγήσει η τιμή της στιγμής αντίστασης στις διαστάσεις του σωλήνα; Μέσω των πινάκων συλλογής που περιέχονται στα GOST 8639-82 και GOST 8645-68 που ρυθμίζουν τις διαστάσεις των τετράγωνων και διαμορφωμένων σωλήνων. Για κάθε μέγεθος, υποδεικνύουν την αντίστοιχη ροπή αντίστασης και για ένα ορθογώνιο τμήμα - κατά μήκος καθενός από τους άξονες.
Αφού ελέγξουμε τους πίνακες, διαπιστώνουμε ότι το ελάχιστο μέγεθος ενός τετράγωνου σωλήνα με τα απαιτούμενα χαρακτηριστικά είναι 50x50x7,0 mm. ορθογώνιο (με κατακόρυφο προσανατολισμό της μεγαλύτερης πλευράς) - 70x30x5,0 mm.

συμπέρασμα
Ελπίζουμε ότι δεν έχουμε καταπονήσει τον αναγνώστη με μια πληθώρα ξηρών φιγούρων και τύπων. Όπως πάντα, πρόσθετες πληροφορίες σχετικά με τις μεθόδους υπολογισμού και σχεδιασμού θόλων από πολυανθρακικό μπορούν να βρεθούν στο βίντεο σε αυτό το άρθρο. Καλή τύχη!
Σας βοήθησε το άρθρο;